23. 合并 K 个升序链表

Similar Question

Solution Tips

方案一: 暴力法

取得值，排序后，重建链表

function ListNode(val){
  this.val = val
  this.next = null
}
var mergeKLists = function(lists) {
  const arr = []
  list.forEach((list) => {
    while(list!==null){
      arr.push(list.val)
      list = list.next
    }
  })
  arr.sort((a,b)=>a-b)
  const val = arr.shift()
  // 边界情况
  if(val===undefined) return null
  const head = new ListNode(val)
  let cur = head
  // 重建链表
  for (let i = 0; i < arr.length; i++) {
    cur.next = new ListNode(arr[i])
    cur = cur.next
  }
  return head
}

复杂度分析

时间复杂度：O(NlogN) ，其中 N 是节点的总数目。

• 遍历所有的值需花费 O(N) 的时间。
• 一个稳定的排序算法花费 O(NlogN) 的时间。
• 遍历同时创建新的有序链表花费 O(N) 的时间。

空间复杂度：O(N)。

• 排序花费 O(N) 空间（这取决于你选择的算法）。
• 创建一个新的链表花费 O(N) 的空间。

方案二: 逐一比较

比较 k 个节点（每个链表的首节点），获得最小值的节点。将选中的节点接在最终有序链表的后面。

复杂度分析

时间复杂度： O(kN) ，其中 k 是链表的数目。

• 几乎最终有序链表中每个节点的时间开销都为 O(k) （k-1 次比较）。
• 总共有 N 个节点在最后的链表中。

空间复杂度：

• O(n) 。创建一个新的链表空间开销为 O(n)。
• O(1) ，重复利用原来的链表节点，每次选择节点时将它直接接在最后返回的链表后面，而不是创建一个新的节点。

方案三: 用优先队列优化方法 2

几乎与上述方法一样，除了将 比较环节 用 优先队列 进行了优化。你可以参考 这里 获取更多信息。

from Queue import PriorityQueue

class Solution(object):
    def mergeKLists(self, lists):
        """
        :type lists: List[ListNode]
        :rtype: ListNode
        """
        head = point = ListNode(0)
        q = PriorityQueue()
        for l in lists:
            if l:
                q.put((l.val, l))
        while not q.empty():
            val, node = q.get()
            point.next = ListNode(val)
            point = point.next
            node = node.next
            if node:
                q.put((node.val, node))
        return head.next

方案四: 逐一两两合并链表

将合并 k 个链表的问题转化成合并 2 个链表 k-1 次。这里是 合并两个有序链表 的题目。

复杂度分析

时间复杂度： O(kN) ，其中 k 是链表的数目。

• 我们可以在 O(n) 的时间内合并两个有序链表，其中 n 是两个链表的总长度
• 把所有合并过程所需的时间加起来，我们可以得到：O(kN)

空间复杂度：O(1)

方案五: 分治

这个方法沿用了上面的解法，但是进行了较大的优化。我们不需要对大部分节点重复遍历多次。

• 将 k 个链表配对，并将同一对中的链表合并
• 重复这一过程，直到我们得到了最终的有序链表。

因此，我们在每一次配对合并的过程中都会遍历几乎全部 N 个节点，并重复这一过程 log2^K 次。

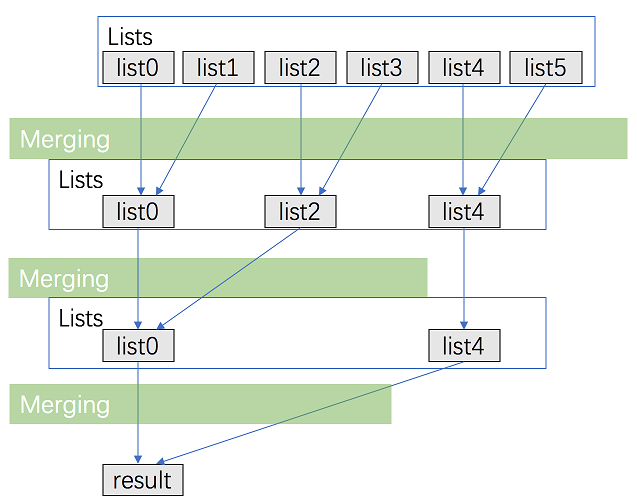
把 list 数组当成队列使用，合并 2 条链表后的重新 push，从头部 shift

function ListNode(val){
  this.val = val
  this.next = null
}
var mergeKLists = function(lists) {
  // 边际情况
  if(lists.length===0) return null
  // 只剩一个链表，停止递归
  if(lists.length===1) return lists[0]

  let l1 = lists.shift(),
      l2 = lists.shift()
  let dummyHead = cur = new ListNode(-1)
  while(l1 && l2){
    if(l1.val<l2.val){
      cur.next = l1
      l1 = l1.next
    }else{
      cur.next = l2
      l2 = l2.next
    }
    cur = cur.next
  }
  if(!l1) cur.next = l2
  else  cur.next = l1
  // 处理头部
  const head = dummyHead.next
  dummyHead.next = null
  lists.push(head)
  return mergeKLists(lists)
}

复杂度分析

• 时间复杂度： O(Nlogk) ，其中 k 是链表的数目
• 空间复杂度：O(1)